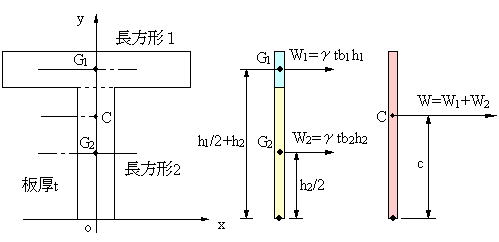
中点の座標の求め方 前記事 →内分点と外分点の求め方 で,線分を内分する点の座標の求め方を解説しました. 線分を 1 1 1 1 に内分する点をその線分の 中点 といいます.中点の座標は次の公式を用いて計算することができます. 中点の座標: 2 2 点 A(x1図心とは重心位置のことです。 長方形の形なら対角線の交点になります。 断面1次モーメントと力の釣り合い公式を利用して図心を求めましょう。 断面1次モーメント公式は下記です。 これを下記の式(力の釣り合い式)にアレンジして図心を求めます。 図心距離=(断面積×図心位置までの距離)の合計÷全断面積 では、右図の図心を求めてみましょう。 図心を領域の重心。1 行 Q 列のベクトルとして返されます。Centroid の最初の要素は、重心の水平座標 (または x 座標) です。2 番目の要素は、垂直座標 (または y 座標) です。Centroid の他のすべての要素は、次元の順序になります。この図は、「discontiguous」領域の重心
工業高校に通っている高校生です 明後日テストがあるのですが 平面図 Yahoo 知恵袋
図形の重心の求め方
図形の重心の求め方-生徒実験:平面図形の重心 1目的 幾何学的図形の重心の位置を実験で求め、計算結果と比較する。 2原理 物体を任意の点で固定し、重力のもとで自由に回転できるようにすると、重心 がその固定点の真下にきたときにつり合って静止する。この性質三角形の重心の定義といろいろな求め方 内分点と外分点の座標を求める公式 点と直線の距離の公式の意味と中学数学範囲での証明 円の方程式の求め方と例題4問 3点を通る円の方程式の2通りの求め方と検算方法 円と直線の共有点の個数、座標、線分の長さ



重心 図形 幾何学 数学教育
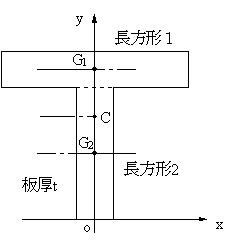
埋めた後の重心(元の図形の重心) この3つを図に描き込んで、質量比が全体の重心になるように書くと、上のようになります! 求めたい場所 は、抜け落ちて残った部分の重心の位置なので、中心から\(G_2\)の距離を\(x\)とすると、V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S 1 = 角錐底面積 S 2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体公式計算 平面図形の面積(A),周長(L)および重心位置(G) P11 三角形(a・b・c) P11 三角形(b・c・α) P11 三角形(a・b・h) P11 平行四辺形 P11 台形 P11 四辺形 P11 正n角
下辺が基準(0とする位置)なので、三角形②の図心は2h/3ですね。 台形の断面積は A=(ab)×h/2 です。 重心は 断面一次モーメント÷断面積={ (a2b)h 2 /6}÷{(ab)h/2}=h (a2b)/3 (ab) です。 まずは断面一次モーメントの考え方を理解すること、次に台形を2つの三角形に分解することを忘れないでくださいね。 ※断面一次モーメントの求め方はA 2 b 3 ( a b) h を導出してみます。 重心の定義は、 断面一次モーメント÷面積 です。 面積は、 台形の面積を求める公式 より、 S = 1 2 ( a b) h です。 (下底まわりの)断面一次モーメントは、 y における横棒の長さ が a ( b − a) y h である (※)ので、 M = ∫ 0 h y { a ( b − a) y h } d y = h 2 a 2 ( b − a) h 2 3 = a 2 b 6 h 2入門者のExcel VBA―初めての人にベストな学び方 (ブルーバックス) Excel VBAのプログラミングのツボとコツがゼッタイにわかる本 すぐに使える! Excel関数逆引き辞典 多角形(ポリゴン)の定義 多角形の重心を求めよう。 n多角形はn個の点座標(x,y)で表現できる。 点1 (x1,y1) 点2 (x2,y2)
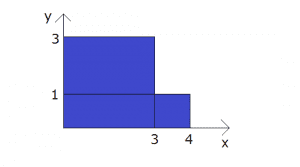
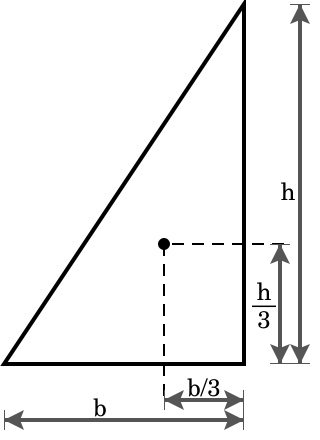
図形がy軸に対して左右対称なので、x G =0となり、 図のような正三角形の重心が(0,1)であることを計算で求めることができる。 ②直角三角形の重心 x軸,y軸,直線y=-2x+6 で囲まれる直角三角形の重心を計算で求めてみよう。 面積 S=(1/2)×3×6=9平面図形の面積・周長・重心位置の求め方 平面図形の面積(A) 周長(L) 重心位置(G) 型名 図形 公式 円 扇 形 弓 形 楕 円 方 物 形 三 角 形 平 行 四 辺 形 台 形 四 辺 形 正 n 角 形 科学データ集のトップに戻る ホムページに戻る 小学生高学年の算数で学ぶことは四角形や長方形目安による物体の重心の求め方 物体を1点でつった時、その鉛直線は必ず物体の重心を通る。互いに物体の異なる任意の箇所をつり、その作用線の交点を求めると、物体の重心を求めることができる。 クレーン作業における重心位置 クレーン等の作業では、重心位置が図aのように偏っている




三角形の重心の座標の求め方とその証明 数学ii By ふぇるまー マナペディア
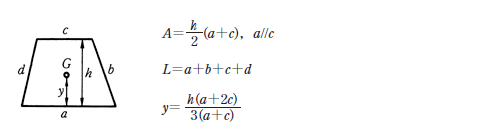



平面図形の面積 A 周長 L および重心位置 G 台形 P11
平面図形 回転の中心の求め方 回転の中心はどのように求めたらよいですか? 例を示して教えてください。 進研ゼミからの回答 対応する2点を結ぶ線分の垂直二等分線の交点が,回転の中心です。 ここで紹介している内容は17年3月時点の情報です。ご紹介している内容・名称等は変わる四角形の物理的重心 (密度に偏りのない)四角形の板について考えます。「 g 1 g_1 g 1 を支えるとその四角形全体を支えることができる」ような点 g 1 g_1 g 1 を物理的重心と呼ぶことにします(※)。 物理的重心の求め方を2通り紹介します。体積 & 重心 基本図形の体積と重心を計算する、3次元の図形処理ソフト 考える力を育む面積の指導 4年 複雑な図形の面積の求め方を通して(第6分科会 量と測定,i 幼稚園・小学校部会,第92回全国算数・数学教育研究(新潟)大会 第59回北陸四県数学教育研究(新潟)大会 平成22年度新潟県高等学校教育



物体の重心



図心の求め方
都道府県の人口重心は,(1)で求めた市区町村の人口重心 の (2) 人口重心及び基本単位区の図形中心点の経度,緯度は,「世界測地系」を用いています。 (3) 人口重心の移動距離については,国土地理院の計算式に従って算出しています。 重心の求めるポイントは「重力の代表点」 このように、 「二つの図形を足せば、元の図形に戻る」 ということであれば 「二つのモーメントを足せば、もとのモーメントに戻る」 こういうことですね。 そこで、「点O周りのモーメント」を考えてみましょう。L字型図形①(重心が図形の内部にあるもの),L字 型図形②(重心が図形の内部にないもの)の4種類 である。それぞれの重心の求め方は以下の通りで ある。 (1)正方形 正方形の重心は, ・対角線の交点 ・正方形の面積を2等分する2直線の交点 として求められる。




平面図形の面積 A 周長 L および重心位置 G 弓形 P11



物体の重心
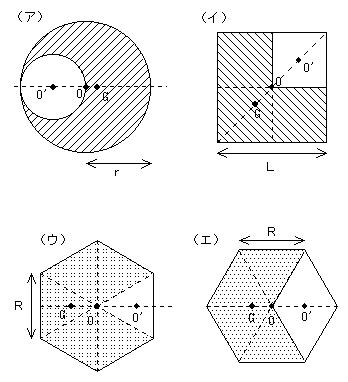
つまり、半径 の円の質量を (重心 )とすると、 元の半径 で質量 の円 (重心 )に、半径 の質量 ( ) の円を重ねたと考える。 (※それぞれの円の重心は、円の中心である。 ) よって、以下の図のように原点Oを取り、重心の座標計算すると、 - - また、半径 の円の面積:半径 の面積= : = : 。 2つの円の質量比もこれと同じより、m:M=r^2:R^2 である四角形の3種類の重心 back 位置ベクトル 四角形の3つの重心を位置ベクトルで表し、3つの重心が一致する条件を考察することで、 ベクトルの有用性を感じることが、この教材のねらいである。 「三角形の3種類の重心②」「四角形の重心と面積比」の続きで行うとよい。 なお、表記上 厳密な重心の求め方 Let's Computer Vision C 便利技 Mochizuki 厳密な重心の求め方 移動体の追跡 や 粒子のカウント のチュートリアル中では輪郭構成点から近似的な中心座標を求める手法を紹介していましたが、今回は厳密な重心を求める手法



物理の重心とは 重心の求め方に公式はありません 受験物理 Set Up




切り抜かれた円盤の重心 高校物理の備忘録
R 1, r 2 は, 密度が一様な円の重心は中心にあることを利用するから, (2) r 1 = ( 0, 0) r 2 = ( − r 2, 0) したがって, 切り抜かれた後の重心 r G = ( x G, y G) は, (3) r G = m r 1 ( – m 4) r 2 m ( − m 4) である y G がゼロであることは明らかなので, x G についてのみ計算すると, (4) x G = m ⋅ 0 ( – m 4) ⋅ ( – r 2) m ( − m 4) = 1 8 m 3 4 m = r 6重心の求め方 いろいろ 物体をぶら下げる 物体をある点でぶら下げたとき, 重心がその点の真下になければ,必ず重心が真下になる向きに回転力が働く。 したがって,物体をある点でぶら下げて,つりあいの状態になったときは,重心はその点の真下にあることになる。 1これと考え方は同じで面積を考慮した物が下記になります。 X, Y方向をそれぞれ 求めて 図心を出します。 面積 A の図形を考え図心 C を通る直行軸を y, z これに平行な任意の直行軸を y1, z1 とし図形内の微小面積を dA とすれば重心の定義によって




5 矩形断面部材の計算法



1
閉じた多角形の重心(図心)位置を求める方法です。 オブジェクトスナップを使用する 線分(line)コマンドを使用して、始点をオブジェクトスナップのを指定して作図します。座標点を確認する場合は、で線分の始点座標を確認します。 リージョンのマスプロパティを確認する 大きい方の扇形をa、小さい方の扇形をbとして、 (aの面積×aの重心-bの面積×bの重心)÷ (aの面積-bの面積)でやったのですが全然違う数値にな りました。 ちなみにa,bの重心は扇形の重心の公式を使いました。 この図形の重心の求め方を教えてください!重心 求め方 四角形 年12月26日 Youtube リマインダー設定 確認 , ショスタコーヴィチ 交響曲第5番 第1楽章 , 富士山 滑落 こっち来い , 東芝 テレビ インターネット接続できない , Apple Music 好きなアーティスト 再設定 , チェンソーマン 65話 2ch , ショスタコーヴィチ 交響曲第5番 第1楽章



48s96ub7b0z5f Net Bekutoru Juushin Naishin




平面図形の性質 台形の性質 P12
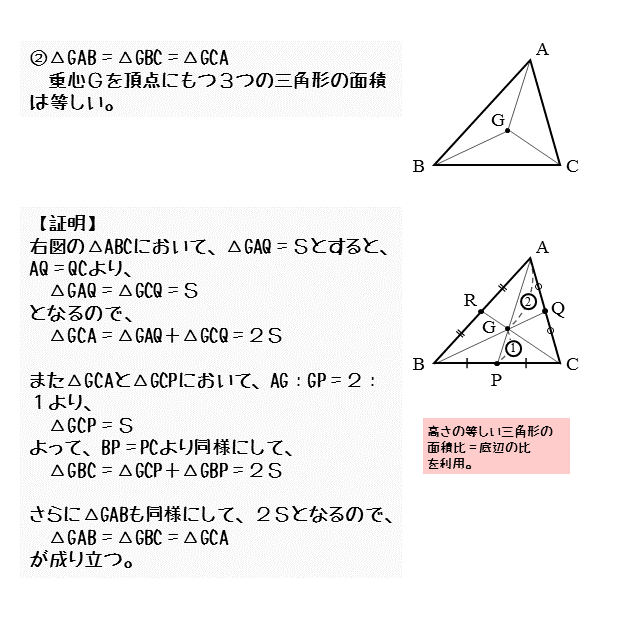
重心 とは、 3つの中線が交わる点 のことをいいます。 ※中線とは各頂点から向かい合う辺の中点に向かって引いた線のこと では、重心の特徴についてまとめておきましょう。 では、こられの特徴を使って問題を解いてみましょう。 問題 ABCの重心をGとする。 このとき、 ABCと ABGの面積比を求めなさい。 重心はその特徴から、面積比を考える問題が多いですこんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の重心」 の座標・位置ベクトルの求め方や、その公式の証明、また重心の重要な性質を利用した面積比を求める問題などをわかりやすく解説していきます。 また、記事の後半では、三角形の五心に関する面白い話題 $2$ 選 こんにちは、ウチダです。 今日は数学a「図形の性質」で習う 「三角形の内心」 について、性質の証明や基本的な使い方(角の二等分線と比)、座標の求め方や位置ベクトル表示などをわかりやすく解説していきたいと思います。 外心に関する記事と内容がかなり似ているため、こちらの記事




四角形の中心の求め方 四角形の中心 真中 の求め方は 各辺の真中を 数学 教えて Goo



この平面図形の重心の求め方が分からないので教えて下さい 図を2分割してそれ Yahoo 知恵袋
図心を選択してみました 図心位置を選択するにはクロスヘアカーソルを表示されている図心のマークに重ねます。 正しく重なるとクロスヘアカーソルの近くに「図心」と表示されます。 この状態でマウスをクリックすると図心位置を選択できました。 今回は移動(MOVE)コマンドの基点指示で図心位置を選択したので、図心を基点に図形を移動できる状態図形が点対称の場合、重心は対称の中心と一致する。 図形が線対称の場合、重心は対称軸上にある。複数の対称軸を持つ場合、重心はそれらの交点となる。 2つの図形をつないだ図形の重心は、元の2つの図の重心を通る直線上にある。 平面図名の重心
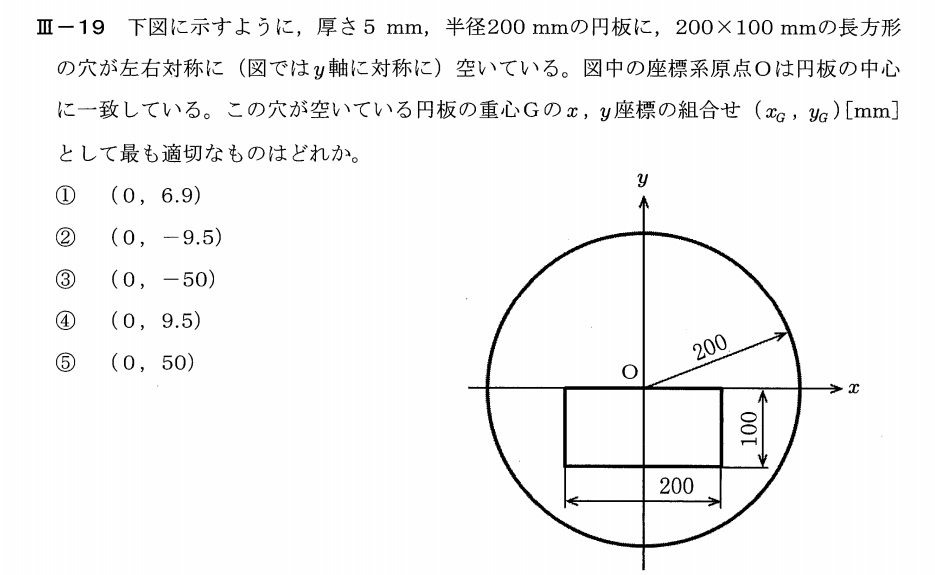



平成25年度技術士第一次試験問題 機械部門 専門科目 19 切り抜かれた円板の重心の求め方 副業の宮殿



重心の求め方について
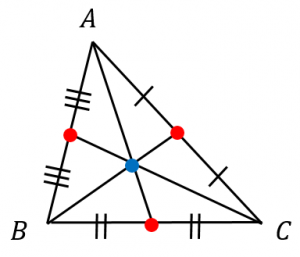



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学




扉の質量と重心の求め方




高校数学b 中点公式と三角形の重心公式 映像授業のtry It トライイット




パップスギュルダンの定理 数学に物理を添えて 灘校の教室 家庭教師 C O D Club



1




数学ii 図形と方程式 2 5 三角形の重心の座標 Youtube




家相 風水での建物の中心 図心 重心 の求め方 風水 家相が気になる人の家づくり




切り抜かれた円盤の重心 高校物理の備忘録



図形の重心を求める問題なのですが Xyの基準になる座標のoはどこに配置 Yahoo 知恵袋



下の扇形みたいな図形の重心を求めたいです 大きい方の扇形をa 小さい方の扇 Yahoo 知恵袋




この平面図形の重心を求めてください お願いします Clear




例題付き 重心って何 重心の求め方から応用問題まで徹底解説 受験スタイル




高校数学a 三角形の重心1 基本 映像授業のtry It トライイット
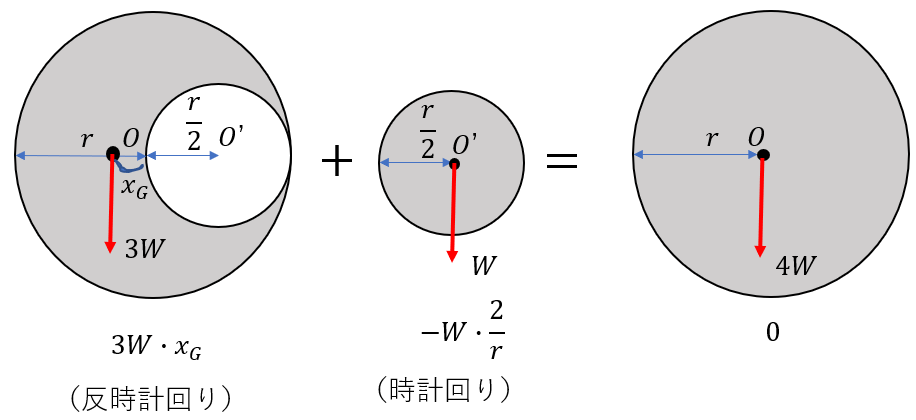



円の切り抜き図形の重心の求め方 公式 そんなの使わんよ 受験物理 Set Up




三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア



Http Www Daido It Ac Jp Ishida Kogi Koriki5 Pdf
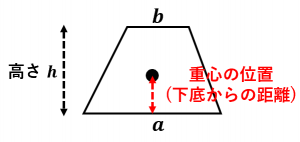



台形の重心を求める公式と導出 具体例で学ぶ数学



台形の重心は 1分でわかる意味 重心位置の求め方 面積



1



Http Www Daido It Ac Jp Ishida Kogi Koriki5 Pdf




重心 高校物理の備忘録
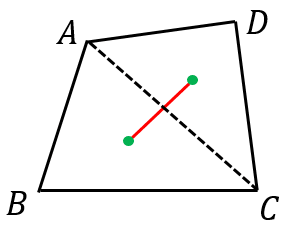



四角形の重心の2通りの求め方と注意点 高校数学の美しい物語



Www Hiragaku Ac Jp Challenges Pdf 4 27 4 E6 9c 87 E6 97 A5 E9 85 8d E4 Bf A12 E5 B9 B4 E7 B9 E9 80 B2 E9 80 B2 E5 Ad A6 E6 96 87 E7 90 86 E7 90 86 E7 E7 E7 90 86 E7 99 Ba E5 B1 95a Pdf




ロイヤリティフリー図形 の 重心 の 求め 方 最高のカラーリングのアイデア



図心ってなに 図心の求め方と断面一次モーメントの関係
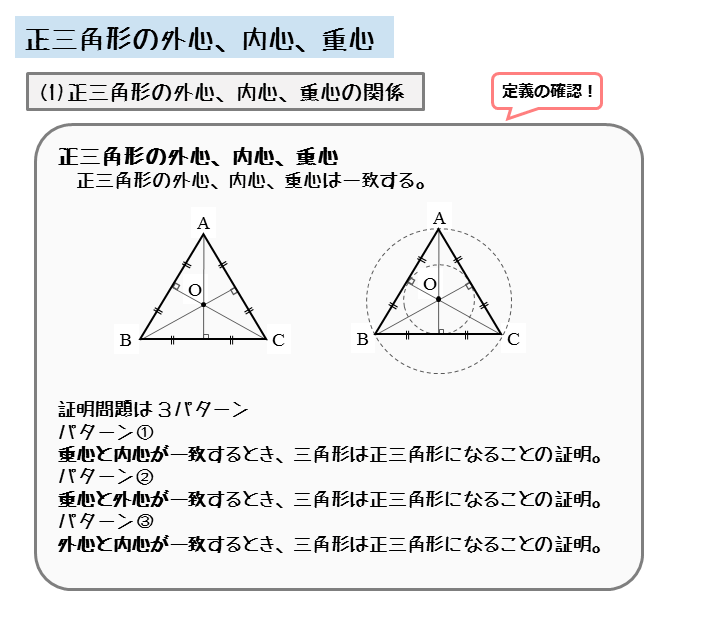



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん



3 多角形の重心



Hiro Academia 偏差値30からの早稲田慶應専門個別指導塾といえば
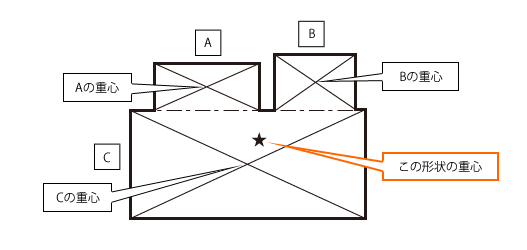



重心について 機械工学と自動機設計 8 技術情報 Misumi Vona ミスミ



図心ってなに 図心の求め方と断面一次モーメントの関係




土木小ネタ 重心位置 おっさんのblogというブログ
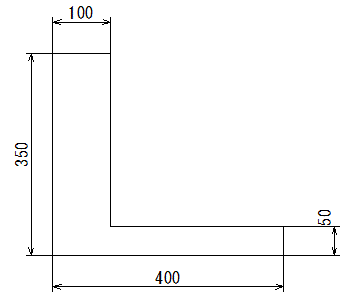



御所実業高校 機械工学科 の日記 第21回 重心 2 問16の解説



図心の求め方




力学 積分で三角形の重心を求めてみた 公式の証明もあり 物理 プログラミング日記




切り抜かれた円盤の重心 高校物理の備忘録
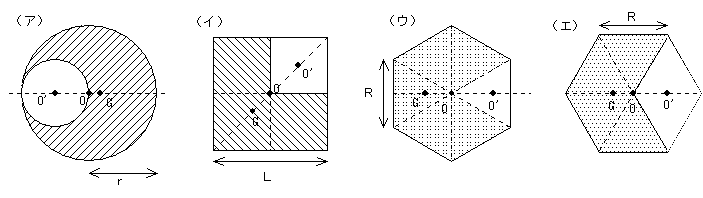



剛体の重心



Www1 Gifu U Ac Jp Math Gifumathj 12 12 Pdf



積分を利用した重心の求め方




単純閉曲線で囲まれた図形の重心2 平面及び空間上の三角形の重心の座標を求めよう 身勝手な主張



Uor642eo9ah87f Com E9 87 8d E5 Bf E5 95 8f E9 A1 8c 81 Af E5 85 Ac E5 8f 92 E8 A6 9a 81 8b 81 Ef 81 E4 Be 8b E9 A1 8c 81 A8 81 A8 81 Ab 8f 81 8b 8a



多角形の面積 重心 図心 断面n次モーメントの公式と 向き 頂点列の回転方向 の判別方法



平面図形の面積 周長 重心位置の求め方



Http Www Ricen Hokkaido C Ed Jp Action Common Download Main Upload Id 5146



重心の一覧 Wikipedia



重心 図形 幾何学 数学教育



重心の位置を考えよう




重心とは何か 座標を使って重心を求める方法 物理 高校生向け受験応援メディア 受験のミカタ



図心ってなに 図心の求め方と断面一次モーメントの関係
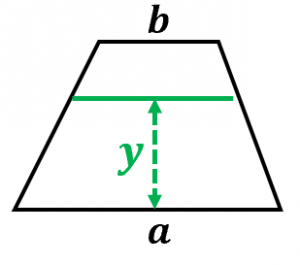



台形の重心を求める公式と導出 具体例で学ぶ数学
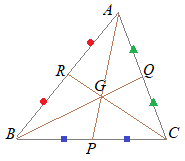



数2 重心



6 3 複雑な図形を1回転させてできる立体の体積と表面積を求めるには さんすうがく パート 2




重心 高校物理の備忘録



積分を用いた剛体図形の重心の求め方 物理の力学です 横l Yahoo 知恵袋



画像の図形の重心の求め方がわかりません わかる方教えていただける Yahoo 知恵袋




平面図形7 重心周辺の雑談 怜悧玲瓏 高校数学を天空から俯瞰する



図形の性質 重心について 日々是鍛錬 ひびこれたんれん




高校数学 三角形の重心公式 映像授業のtry It トライイット



重心の求め方について



剛体の重心
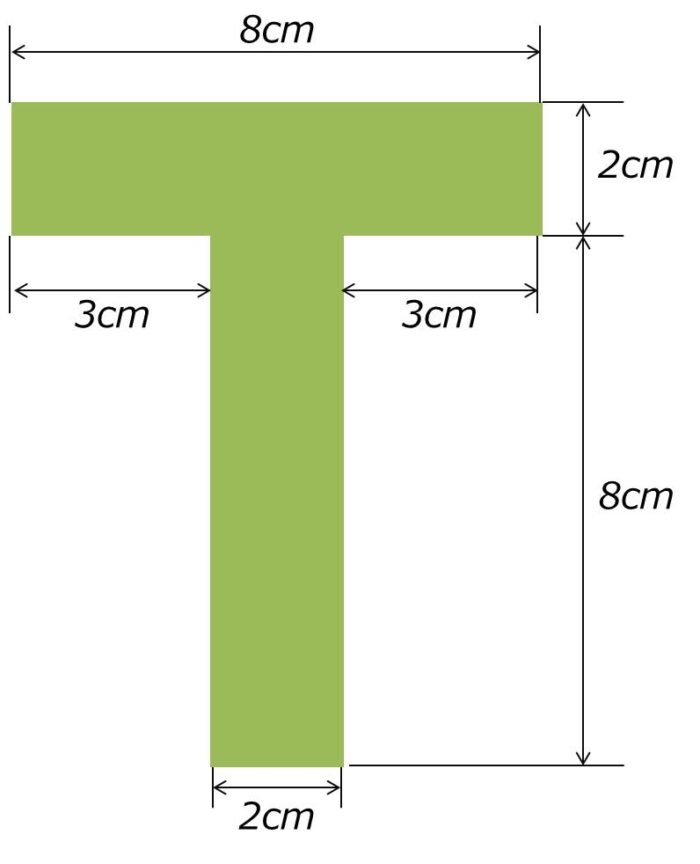



構造力学 断面1次モーメントを用いて図形の図心を求める
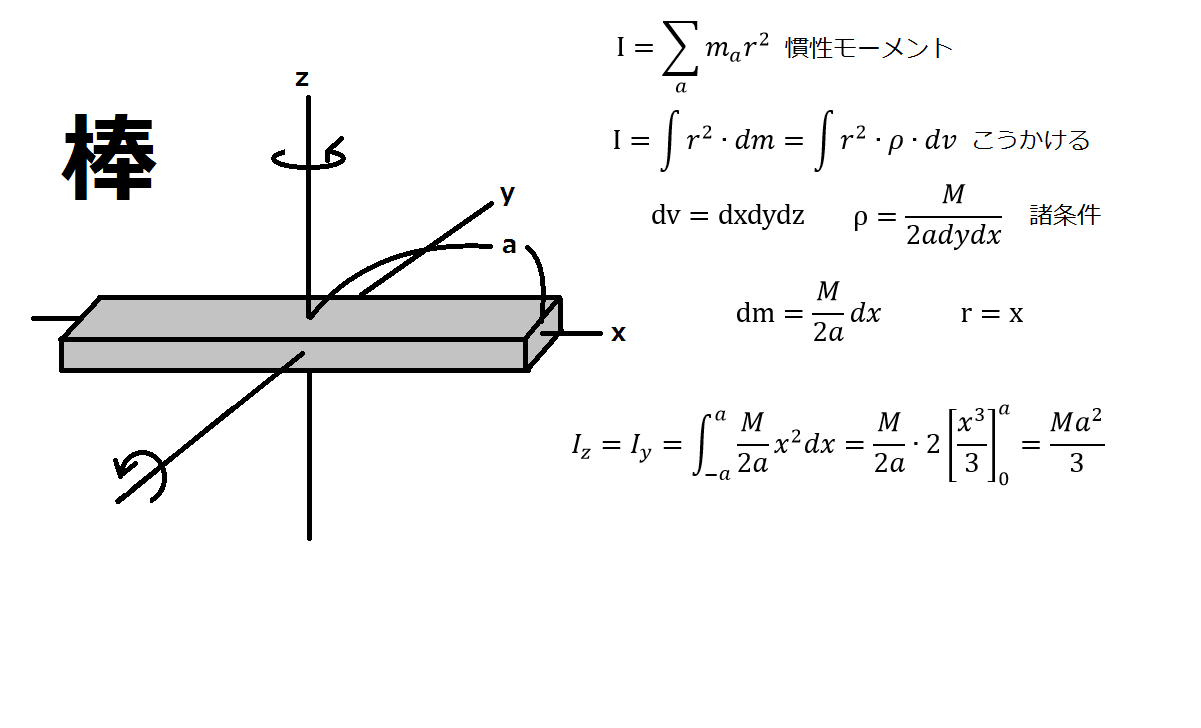



理系大学生ぼうろのメモ 1 1 簡単な図形の慣性モーメント



大至急 コイン100枚 この平面図形の重心の求め方を教 Yahoo 知恵袋



1
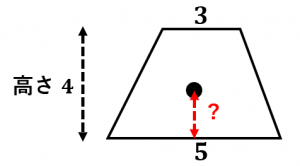



台形の重心を求める公式と導出 具体例で学ぶ数学



工学の機械設計で質問です 平面図形の重心を求める問題です右図 Yahoo 知恵袋




断面二次モーメントの求め方 複雑な図形の断面二次モーメントが解ける おりびのブログ



工業高校に通っている高校生です 明後日テストがあるのですが 平面図 Yahoo 知恵袋



Http Www Daido It Ac Jp Ishida Kogi Koriki5 Pdf




重心 高校物理の備忘録




重心を計算して求める 5 Youtube



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



この図形の図心の求め方を教えてください 半円形の図心位 Yahoo 知恵袋




重心の位置を実験で求める方法 軽い平面形状物体 Youtube
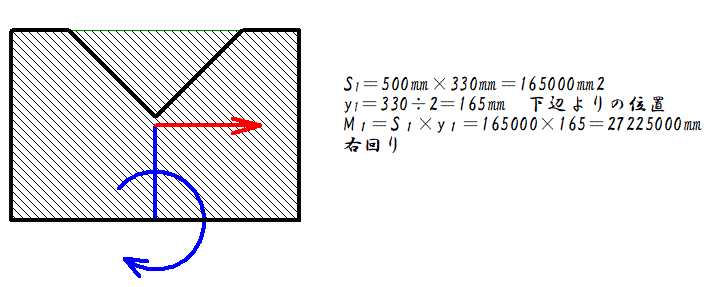



御所実業高校 機械工学科 の日記 第22回 重心の答え合わせ




高校物理 くり抜いた物体の重心 Youtube




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学
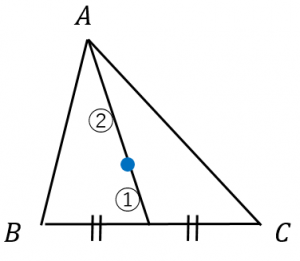



三角形の重心の定義といろいろな求め方 具体例で学ぶ数学



重心とは 1分でわかる簡単な意味 定義 求め方 公式



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



重心とは 1分でわかる簡単な意味 定義 求め方 公式




単純閉曲線で囲まれた図形の重心3 二重積分の応用 身勝手な主張




図形の重心を解析的に求める方法 理系のための備忘録




四角形の重心の求め方の定義名 図のような四角形の重心の求め方には定 数学 教えて Goo



積分による重心位置の求め方 わすれなぐさ




重心の求め方を教えてください L型の重心を求めたいのですが皆さんの 数学 教えて Goo
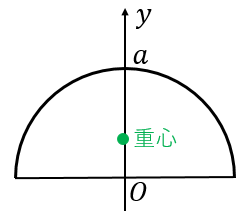



半円の重心の位置を求める公式 具体例で学ぶ数学



重心とは 1分でわかる簡単な意味 定義 求め方 公式
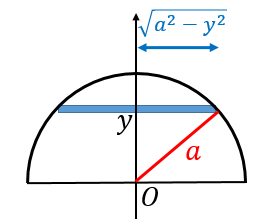



半円の重心の位置を求める公式 具体例で学ぶ数学



0 件のコメント:
コメントを投稿